| 一問一答クイズ [No.10010] | |
|---|---|
 公式・方程式検定 より
算数や数学で習った図形の面積を求める公式や方程式の問題です。みなさん、ちゃんと覚えているでしょうか？
|
|
 三角形の面積を求める公式は？ |
|
| 制限時間 ： 無制限 | |
| 難易度 |  |
| 出題数 | 2727人中 |
| 正解数 | 2484人 |
| 正解率 | 91.09％ |
| 作成者 | ゆうじ （ID:53） |
| 最高連続正解数 | 0 問 |
| 現在の連続記録 | 0 問 ※ユーザーの方は記録が更新されます |
登録タグ
関連するクイズ・検定
- 1. 算数トレーニング（小学生）
- 2. 数列穴埋めクイズ
- 3. クイック掛け算検定
- 4. 素数検定（初級編）
- 5. 数学３級検定
- 6. 数学雑学クイズ
- 7. 難問数学
- 8. 英数理社国 クイズ
- 9. クイック足し算検定
- 10. 数列クイズ
- 11. 確率問題
- 12. 計算検定(激ムズ)
- 13. 数列検定
- 14. 中１で習う数学 その二
- 15. 数学検定
- 16. クイック引き算検定
- 17. おつりはいくらテスト
- 18. 中１ 数学の基礎?
- 19. けーさんけんてー
- 20. 全問正解間違いなしクイズ
その他のクイズ・検定
予習・復習／一問一答クイズ出題文をクリックするとクイズにチャレンジできます。
すぐに答えを見たい場合は「解答を表示する」をクリックしてください。
こちらで学習をして、このクイズ・検定の合格を目指しましょう！
すぐに答えを見たい場合は「解答を表示する」をクリックしてください。
こちらで学習をして、このクイズ・検定の合格を目指しましょう！
①(上底＋下底)×高さ
②(上底＋下底)×高さ÷2
③底辺×高さ÷2
④（底辺×高さ）−２
解答を表示する
正解：②
①半径×半径
②円周÷円周率÷2
③直径×円周率
④底辺×高さ
解答を表示する
正解：半径×半径×円周率
①半径×半径×円周率
②時間÷道のり
③道のり÷速度
④道のり×時間
解答を表示する
正解：道のり÷時間
①道のり÷時間
②E=mc二乗
③E=m＋c
④E=mc
解答を表示する
正解：②
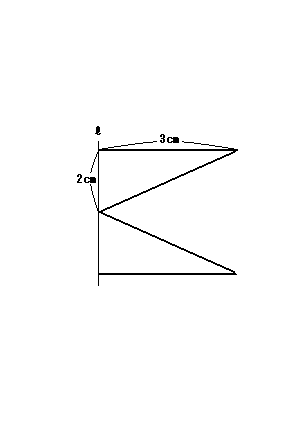
①10πcm3
②12πcm3
③18πcm3
④E=m÷c
解答を表示する
正解：②
解説：回転体の公式（底面積×高さ）で、円錐の体積はこれを３でわると出てくるので、 ３×３×π×２÷３＝６π・・・? ?が2個あるので、 Ａ.12cm3（立方センチメートル）
①底面積×高さ÷3.14
②24πcm3
③底面積×高さ
④底面積×高さ÷３
解答を表示する
正解：④
①半径×半径×高さ
②半径×半径×円周率×高さ÷２（=底面積×高さ÷２）
③底面積×高さ÷２
④半径×半径×円周率×高さ（=底面積×高さ）
解答を表示する
正解：④
①240度×(n-1)
②360度×(n-2)
③180度×(n-1)
④半径×円周率×高さ
解答を表示する
正解：180度×(n-2)
①180度×(n-2)
②180度×(n+2)
③360度（公式はない）
④180度×(n-2)
解答を表示する
正解：③
①対角線×対角線÷２
②360度×(n-1)
③一辺×一辺
④一辺×一辺÷２
解答を表示する
正解：①
①2sinθcosθ
②2cos2乗θ-1
③1-sin2乗θ
④cos2乗θ-sin2乗θ
解答を表示する
正解：①
解説：2sinθcosθはsin2θと同値です。
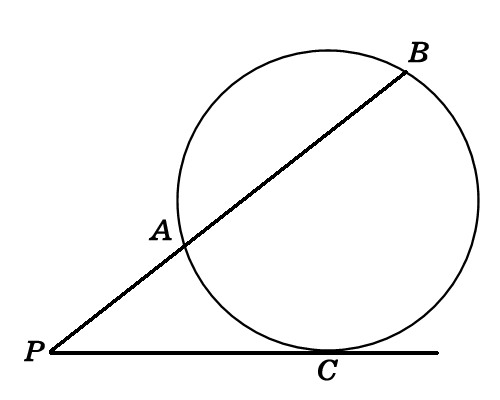
①3√3
②2√2
③3√2
④対角線×対角線
解答を表示する
正解：2√3
①2√3
②ｘ＝2 ｙ＝-1/6
③ｘ＝1 ｙ＝1
④ｘ＝-1 ｙ＝7/3
解答を表示する
正解：上記の方程式を満たす解は存在しない。
解説：グラフを書いてみれば納得できるでしょう 。
①30
②29
③31
④32
解答を表示する
正解：④
解説：6の41乗の常用対数をとれば、x=10により、41(logx2＋logx3)＝41(0.3010+0.4771)＝31.9021となり、31＜logx6の41乗＜32より、32桁と解ります。
①sinαsinβ＋cosαcosβ
②上記の方程式を満たす解は存在しない。
③sinα＋sinβ
④sinαcosα＋sinβcosβ
解答を表示する
正解：sinαcosβ＋cosαsinβ
その他・関連するクイズこのクイズ・検定や問題に関連するクイズを出題しております。出題文をクリックするとクイズにチャレンジできます。
すぐに答えを見たい場合は「解答を表示する」をクリックしてください。
すぐに答えを見たい場合は「解答を表示する」をクリックしてください。
以下のクイズは、全問正解間違いなしクイズより、出題しております。
説明：足し算の簡単問題です 全問正解間違いなし
①４
②３
③５
④２
解答を表示する
正解：④
①４
②６
③５
④sinαcosβ＋cosαsinβ
解答を表示する
正解：①
①７
②９０
③２
④０
解答を表示する
正解：④
①１
②０
③３
④１
解答を表示する
正解：③
①３
②５
③２
④４
解答を表示する
正解：②
①００
②２
③３
④２
解答を表示する
正解：③
①１
②７
③８
④９
解答を表示する
正解：④
①１１
②５
③５５
④０９
解答を表示する
正解：②
①４
②９
③８う
④８
解答を表示する
正解：②
①１０
②２
③８
④７
解答を表示する
正解：①
①９
②１２３
③２０
④１O
解答を表示する
正解：１０
①２２
②１０
③１１
④３３
解答を表示する
正解：③